【第一部分方法指导】
计算型选择题一般有两类。一类是题中提供信息材料,需要应用地理概念、原理、规律来解决问题。如区时与地方时、昼夜长短与正午太阳高度计算、日出日落时刻计算、比例尺、人口自然增长率、城市化水平等。这类题除需临发挥外,更需要考生在平时加深对概念的理解,狠抓规律和原理的应用。另一类是题中提供信息材料和新的计算公式,要求考生用其来解决实际问题。这类题在试卷中出现较多,往往会给出如日照间距、人口生理密度、人口耕地面积等新概念。对这些新概念,考生必须仔细分析,充分理解,然后再进行应用。
1.地球运动地理意义相关计算
地球自转,东早西晚,1度4分,东加西减,经经计较,分秒必算。
②计算时具体可分为四个步骤:一定时,二定向,三定差,四定值。
|
|
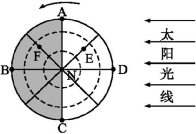
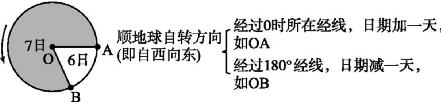
昼、夜半球中央经线的地方时分别为12时、24时(或0时),如ND、NB所在经线;晨、昏线与赤道交点所在经线的地方时分别为6时、18时,如NC、NA所在经线
|
|
|
图中求E点的地方时,以D点作为已知时间点,则E点位于D点以东,应选择“东加”;若求F点的地方时,以B点作为已知时间点,则F点位于B点以西,应选择“西减”
|
|
|
|
|
四定值,所求的地方时=已知地方时±4分钟×经度差/1°
|
如以D点作为已知时间点求E点的地方时为12:00+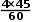 =15:00,以B点作为已知时间点求F点的地方时为24:00— =15:00,以B点作为已知时间点求F点的地方时为24:00—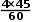 =21:00 =21:00
|
(2)区时的计算
|
|
若已知某地经度,可根据经度确定出所在的时区,方法为:该地的经度数&pide;15°,所得余数若小于7.5°,则商为该地所在时区数,若余数大于7.5°,则商+1为该地所在时区数;东西时区根据东西经确定
|
|
|
如果两地分别在东、西时区,则东时区在东,西时区在西。如果两地都在东时区,区号大的在东,区号小的在西;两地都在西时区,区号大的在西,区号小的在东
|
|
|
如果两地分别在东、西时区,相差的时区数即为两区号相加。如果两地都在东时区或西时区,相差的时区数即为两区号相减
|
|
四定值,所求时区的区时=已知时区的区时±时区差×1小时
|
如当东八区为18:00时,西五区为18—13=5:00;当中时区为3:00时,东三区为3+3=6:00
|
①经度差:两地同为东(西)经,取两数之差;一地为东经,另一地为西经,取两数之和。
②时区差:两地同在东(西)时区,取两数之差;一地在东时区,另一地在西时区,取两数之和。
先画出表示全球所有经线(或时区)的数轴,标出已知经线(或时区)及其地方时(或区时),再标出所求经线(或时区),计算出两地经度差(或时区差)后,再将其转化为地方时差(或区时差)。如下图所示。
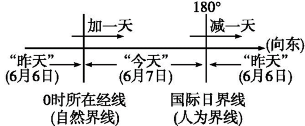
(3)日期变更顺着地球自转的方向,过0时所在经线日期要加一天,过国际日界线日期则要减一天。如下图所示:
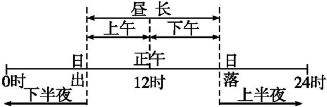
一个地区一天的日出和日落时间反映了该日的昼夜长短状况。白昼以12时为界,上午与下午时间间隔相等;黑夜以午夜(0时或24时)为界,上半夜与下半夜时间间隔相等。
因此已知某地某一天的昼长,可求出该日的日出、日落时间(地方时),其方法为:
日出时间=12—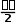 ;日落时间=12+
;日落时间=12+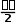 相反,根据某地某一天日出、日落时间可计算昼长、夜长,其方法为:
某地昼长=日落时间—日出时间=(正午12时—日出时间)×2=(日落时间—正午12时)×2
某地夜长=(子夜24时—日落时间)×2=(日出时间—子夜0时)×2
方法:昼长=白昼弧度数/15°,即在日照图上某条纬线与晨昏线有两个交点,两点之间在昼半球的弧度数/15°,就是白昼的时长。
公式:H=90°—|当地地理纬度±太阳直射点所在纬度|
“±”:若两点同在南半球或北半球,用减法;若两点分属于南、北半球,用加法。
从等高线图上读出任意两点的海拔,就可以计算这两点的相对高度:H相=H高-H低。
估算方法:一般说来,若在等高线地形图上,任意两点之间有n条等高线,等高距为d,则这两点的相对高度H相可用下面公式求算:(n-1) d<H相<(n+1)d(注:此公式仅适用于单调递增或单调递减等高线图)。
公式:(n-1)≤H<(n+1)d(n:为重叠等高线条数;d为等高距。)
公式:h大≤h顶< h大+d(h顶:陡崖顶部海拔高度;h大:重叠等高线中的最大数值;d为等高距。)
公式:h小—d <h底≤ h小(h底:陡崖底部海拔高度;h小:重叠等高线中的最小数值;d为等高距。)
比例尺=图上距离&pide;实际距离.(在比例尺计算中要注意单位间的换算)
(1公里=1千米=1×1000米=1×100000厘米)
(1)同一纬线上两地,根据经度差计算距离:L=经度差×111千米/度×cosα(α为该纬线的纬度)
同一经线上两地,根据纬度差计算距离:L=纬度差×111千米/度。
(2)不同经线和纬线上:计算两点间距离时可进行估算。
一是可以先假设两点的经度相同或纬度相同,然后再根据实际情况扩大或缩小;
例题1 (2023·广东省东源中学模拟预测)某中学地理研学小组到华北某地进行研学。该地正在打造“太阳山”工程——建设大型山坡集中式光伏发电站,下图示意该地等高线分布(单位:m)。据此完成下面小题。
【解析】1.读图可知,桥梁位于瀑布上游地区,瀑布的高差约为52 m,图中等高距为100米, 则可计算出桥梁的海拔高度约为352~400m,山峰的高度为915m,则二者的高差应当为515~563m, 所以B正确。ACD错误。故选B。
2.山峰的海拔高度用目测不可能准确,A错误。甲地坡面径流流向东北,因为东北地势更低,B错误。甲丁之间没有东西遮挡,所以甲地可观测到丁地植被,D正确。欣赏瀑布的最佳地点是在一定的距离和角度仰视,桥梁的海拔比瀑布高,不是最佳欣赏地点,C错误。故选D。
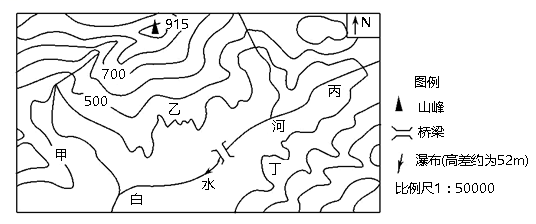
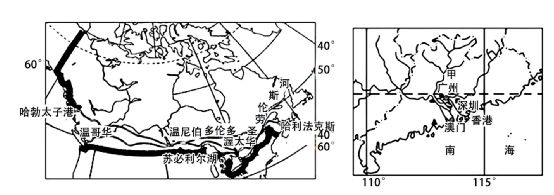
例题2 (2023·江西·赣州市赣县第三中学模拟预测)孟晚舟乘坐中国政府包机于9月24日16时29分(当地区时,采用的夏令时)从加拿大温哥华(49°13'N,123°06'W)机场起飞,于北京时间9月25日21时51分降落在中国深圳宝安机场(22°32'N,114°03'E)(下图)。孟晚舟在飞机上感言:“此刻飞机正飞在北极……正是那一抹绚丽的中国红……引领我回家的漫长路途。”读下面两幅图,据此完成问题。
【解析】根据材料可知,起飞时间按照西八区区时计算,但由于是夏令时,所以实际当时西八区区时是15时29分,然后飞到深圳,用的是北京时间,时区相差16小时,用25日21时51分减去16小时,得出降落时的温哥华时间25日5时51分,再减去起飞时的温哥时间24日15时29分,得出14时22分,C正确,ABD错误。故选C。
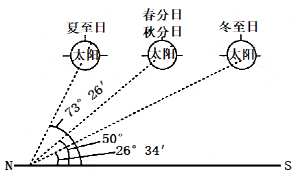
例题3 (2023·陕西·安康市教学研究室二模)读我国某城市二分二至日正午太阳高度分布示意图,完成下面小题。
【解析】由当地正午太阳高度角=90度—|当地的地理纬度和太阳直射点纬度之间的差|公式可知,春秋分时太阳直射赤道,此时当地正午太阳高度角为50°,故当地的地理纬度=90°—50°=40°,故C正确,故选C。
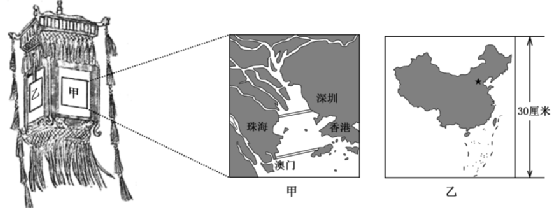
例题4 (2019·北京·高考真题)某中学制作主题为“点亮中国”的宫灯,下图为学生手绘的设计图。读图,完成下面小题。
【解析】中国国土北起黑龙江省漠河以北的黑龙江主航道中心线(北纬53°多),南至南沙群岛中的曾母暗沙(北纬4°附近),南北相距约5500公里;该地图图上距离约30厘米,则比例尺为30厘米/5500千米=1/183千米≈1/200千米。故答案为B。
(2023·江西省安义中学三模)北京时间3月23日15:40神舟十三号的3名航天员在中国空间站讲授了“天宫课堂”第二课。据此完成下面小题。
1.3月23日“天宫课堂”开讲时,在伦敦留学的小明手表时间是()
【解析】1.据材料可知,北京时间3月23日15:40神舟十三号的3名航天员在中国空间站讲授了“天宫课堂”第二课,北京时间即东八区区时,据所学知识可知,伦敦位于零时区,两地相差8个时区,所以按照“东加西减”的方式,3月23日“天宫课堂”开讲时,在伦敦留学的小明手表时间为23日7时40分,A正确;BCD错误。故选A。
(2023·河南·模拟预测)北京时间2022年4月16日09时56分,神舟十三号载人飞船返回舱在内蒙古东风着陆场成功着陆,着陆点中心地理坐标为(41°37'43”N,100°04'28”E)。现场医监医保人员确认航天员翟志刚、王亚平、叶光富身体状况良好,神舟十三号载人飞行任务取得圆满成功。据此完成下面小题。
2.神舟十三号载人飞船返回当日,与内蒙古相比,云南()
4.三位航天员重返地面时,与北京处于同一日期的范围占全球范围的比例()
【解析】2.地球自转角速度,在地球上除极点外,各地都相同,A错误;云南所处纬度比内蒙古低,4月太阳直射点位于北半球,云南距离太阳直射点更近,正午太阳高度更大,B正确;自转线速度由赤道向两极递减,因此云南比内蒙古线速度大,C错误;太阳直射点位于北半球,北半球纬度越高昼越长,内蒙古昼更长,D错误。故选B。
3.国际标准时为0时区,北京时间2022年4月16日09时56分,即东八区为4月16日09时56分,0时区位于东八区西侧且相差八个小时,根据“东加西减”,国际标准时间为2022年4月16日1:56,A正确。故选A。
4.北京时间2022年4月16日09时56分,即东经120度的地方时,此时对应180度经线的地方时为4月16日09时56分+4小时=4月16日13时56分,则4月16日占全球的比例为13时56分/24小时,约为7/12。B正确。故选B。
(2021·天津·高考真题)科考队在北极圈内某地进行科考时,于北京时间6月22日16时测得了当地一天中太阳高度的最小值为10°。完成下面小题。
【分析】5.6月22日是夏至日,太阳直射点位于北回归线,该地为北极圈以内,有极昼,一天中最小太阳高度为10°,为0:00的太阳高度,此时北极圈上0:00的太阳高度0°,从而得出该地的纬度为北极圈以北10°,即76°34′N,故C项正确,ABD错误。故选C。
6.由材料可知,此时为6月22日(夏至日),北极圈及其以北地区出现极昼现象,因此该地出现一天中最小太阳高度时,地方时应为24时,而此时北京时间为16时,说明与北京所在时区相差八个时区,每时区经度相距15°,由此可得出该地经度约为120°W,选项中符合条件的只有北美北部。故A,B,C项错误,D项正确。故选D。
【点睛】极圈内刚好发生极昼的纬度与直射点纬度互余,该纬度0:00的太阳高度为0°,如果给出极圈内某地0:00的太阳高度,求该地的纬度,就将刚好发生极昼的纬度加上该地0:00的太阳高度,就可以得出该地的纬度。
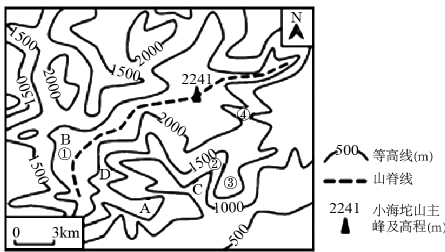
(2023·江苏·模拟预测)小海坨山位于延庆县西北部,呈东南——西北走向,是2022年北京冬奥会的重要赛区之一。读下图,完成下面小题。
7.图示区域最高点为小海坨主峰,海拔为2241米,最低点位于图示区域东南,海拔为0~500米。因此图示区域最大海拔差可能是接近2241米,D正确,ABC错误。故选D。
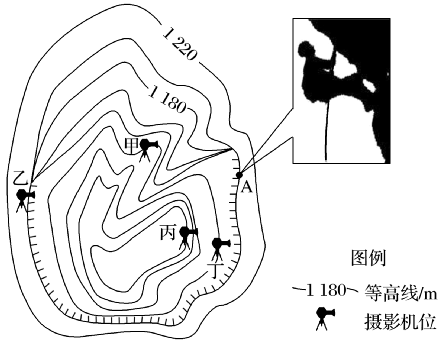
(2023·全国·模拟预测)下图是“我国某地附近等高线图及某绳降照片”。读图,完成下面小题。
8.某极限运动俱乐部在A处从崖顶到崖底开展绳降比赛,运动员准备的绳长最适宜的是()
【分析】8.图中等高距为20米,A处有四条等高线重叠,则该处陡崖相对高度介于60至100米之间,为安全考虑,绳长应略大于100米较合适,B正确,ACD错误。故选B。
(2021·北京·高考真题)我国某镇利用当地主产的粮食制作粮画,打造粮画小镇。图a是M学校设计的小镇地理位置指示牌,图b是该校设计的四条“行走的思政课”精华路线示意图。读图,完成下面小题。
【解析】9.图中最短精华路线是从M学校至传统民居保护地这条线路,根据图中比例尺进行计算,图上1厘米代表实际距离5千米,可以计算出最短的精华路线里程约为10千米,B项正确。故选B。
【点睛】比例尺计算公式:实际距离=图上距离&pide;比例尺
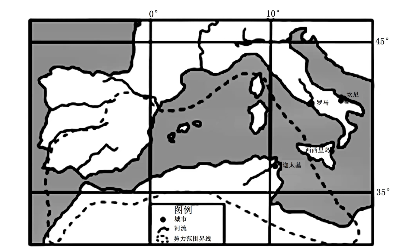
(2023·全国·模拟预测)公元前814年,以航海经商著称的腓尼基人兴建迦太基城。公元前264年为争夺海上交通枢纽西西里岛,与罗马帝国交战失败,史称“第一次布匿战争”。公元4~16世纪期间迦太基沦为拜占庭等国家属地,迦太基商贸地位逐渐衰落。下图为迦太基势力范围示意图。据此完成下面小题。
10.从罗马经西西里岛西端至迦太基的最短距离约()
【解析】10.根据题意观察图中信息,罗马到迦太基的距离大约跨越纬度5°(按照跨越35°-45°大约估算),而地球的经线圈都是相同的周长,主要以本初子午线所在经线圈计算,大致为40007千米,一周为360°,则跨越1°纬度实际长度大约为111千米,则罗马到迦太基的最短距离大约为111.1×5≈555千米,ABCD四个选项中,只有B选项500千米最接近答案,故B正确。答案选择B。
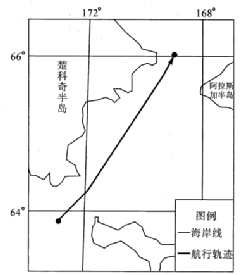
(2023·北京·模拟预测)下图为某年7月赴北极科考的“雪龙二号”科考船的一日航行轨迹图。读图,完成下列小题。
【解析】11.根据图中信息,该日“雪龙二号”的航行路径大致跨越了两个纬度,四个经度,大致可以得出其两个直角边的距离为222km左右,线路为其斜边,约为300km左右,C正确,ABD选项均差距过大。故选C。
(2021·江苏·高考真题)公元8世纪开始,基尔瓦逐渐成为非洲东海岸的商贸中心。15世纪初郑和船队曾从不同航线到达基尔瓦。17、18世纪随着世界贸易格局不断改变,基尔瓦商贸地位逐渐衰落。1981年基尔瓦所在地的遗址被列入世界遗产名录。图为“郑和船队航海路线示意图”。据此完成下面小题。
12.郑和船队若每天航行190km,从科伦坡经摩加迪沙至基尔瓦的最短时间约()
【解析】12.据图中经纬线可知,从科伦坡到摩加迪沙大致经过35个经度距,且位于赤道附近,故两地距离可计算为111×35=3885km,从摩加迪沙到基尔瓦大致经过10个纬度距,可计算两地距离为10×111=1110km,故从科伦坡到基尔瓦距离大致为4995km,据材料,郑和船队每天航行190km,可计算大致需要27天能到达,故最短4周就可到达,B项正确,ACD错误。故选B。
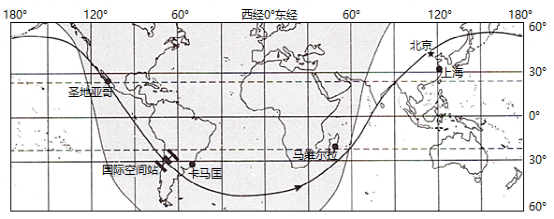
(2022·江苏·高考真题)国际空间站距地面约420km,每90分钟环绕地球一周。空间站反射阳光,在一定条件下,人们肉眼可以看到明亮的光点划过天空。下图为“国际空间站某时段轨迹和某时刻位置示意图”,图中阴影表示黑夜。据此完成下面小题。
【解析】13.由图可知北京与国际空间站经度大致相差180°,所以国际空间站到达北京上空是大致绕地球旋转了一半,由材料可知国际空间站每90分钟环绕地球一周,所以空间站到达北京上空约需45分钟。故C正确ABD错误。故答案选C。
14.由下图可知图中A点与120°E相距约为60°,A点为晨线与赤道的交点,则A点地方时为6时,则北京时间此时约为10:00,结合上面分析,可知空间站到达北京上空时,北京时间大致为10:45,故C正确ABD错误。故答案选C。
相反,根据某地某一天日出、日落时间可计算昼长、夜长,其方法为:
某地昼长=日落时间—日出时间=(正午12时—日出时间)×2=(日落时间—正午12时)×2
某地夜长=(子夜24时—日落时间)×2=(日出时间—子夜0时)×2
方法:昼长=白昼弧度数/15°,即在日照图上某条纬线与晨昏线有两个交点,两点之间在昼半球的弧度数/15°,就是白昼的时长。
公式:H=90°—|当地地理纬度±太阳直射点所在纬度|
“±”:若两点同在南半球或北半球,用减法;若两点分属于南、北半球,用加法。
从等高线图上读出任意两点的海拔,就可以计算这两点的相对高度:H相=H高-H低。
估算方法:一般说来,若在等高线地形图上,任意两点之间有n条等高线,等高距为d,则这两点的相对高度H相可用下面公式求算:(n-1) d<H相<(n+1)d(注:此公式仅适用于单调递增或单调递减等高线图)。
公式:(n-1)≤H<(n+1)d(n:为重叠等高线条数;d为等高距。)
公式:h大≤h顶< h大+d(h顶:陡崖顶部海拔高度;h大:重叠等高线中的最大数值;d为等高距。)
公式:h小—d <h底≤ h小(h底:陡崖底部海拔高度;h小:重叠等高线中的最小数值;d为等高距。)
比例尺=图上距离&pide;实际距离.(在比例尺计算中要注意单位间的换算)
(1公里=1千米=1×1000米=1×100000厘米)
(1)同一纬线上两地,根据经度差计算距离:L=经度差×111千米/度×cosα(α为该纬线的纬度)
同一经线上两地,根据纬度差计算距离:L=纬度差×111千米/度。
(2)不同经线和纬线上:计算两点间距离时可进行估算。
一是可以先假设两点的经度相同或纬度相同,然后再根据实际情况扩大或缩小;
例题1 (2023·广东省东源中学模拟预测)某中学地理研学小组到华北某地进行研学。该地正在打造“太阳山”工程——建设大型山坡集中式光伏发电站,下图示意该地等高线分布(单位:m)。据此完成下面小题。
【解析】1.读图可知,桥梁位于瀑布上游地区,瀑布的高差约为52 m,图中等高距为100米, 则可计算出桥梁的海拔高度约为352~400m,山峰的高度为915m,则二者的高差应当为515~563m, 所以B正确。ACD错误。故选B。
2.山峰的海拔高度用目测不可能准确,A错误。甲地坡面径流流向东北,因为东北地势更低,B错误。甲丁之间没有东西遮挡,所以甲地可观测到丁地植被,D正确。欣赏瀑布的最佳地点是在一定的距离和角度仰视,桥梁的海拔比瀑布高,不是最佳欣赏地点,C错误。故选D。
例题2 (2023·江西·赣州市赣县第三中学模拟预测)孟晚舟乘坐中国政府包机于9月24日16时29分(当地区时,采用的夏令时)从加拿大温哥华(49°13'N,123°06'W)机场起飞,于北京时间9月25日21时51分降落在中国深圳宝安机场(22°32'N,114°03'E)(下图)。孟晚舟在飞机上感言:“此刻飞机正飞在北极……正是那一抹绚丽的中国红……引领我回家的漫长路途。”读下面两幅图,据此完成问题。
【解析】根据材料可知,起飞时间按照西八区区时计算,但由于是夏令时,所以实际当时西八区区时是15时29分,然后飞到深圳,用的是北京时间,时区相差16小时,用25日21时51分减去16小时,得出降落时的温哥华时间25日5时51分,再减去起飞时的温哥时间24日15时29分,得出14时22分,C正确,ABD错误。故选C。
例题3 (2023·陕西·安康市教学研究室二模)读我国某城市二分二至日正午太阳高度分布示意图,完成下面小题。
【解析】由当地正午太阳高度角=90度—|当地的地理纬度和太阳直射点纬度之间的差|公式可知,春秋分时太阳直射赤道,此时当地正午太阳高度角为50°,故当地的地理纬度=90°—50°=40°,故C正确,故选C。
例题4 (2019·北京·高考真题)某中学制作主题为“点亮中国”的宫灯,下图为学生手绘的设计图。读图,完成下面小题。
【解析】中国国土北起黑龙江省漠河以北的黑龙江主航道中心线(北纬53°多),南至南沙群岛中的曾母暗沙(北纬4°附近),南北相距约5500公里;该地图图上距离约30厘米,则比例尺为30厘米/5500千米=1/183千米≈1/200千米。故答案为B。
(2023·江西省安义中学三模)北京时间3月23日15:40神舟十三号的3名航天员在中国空间站讲授了“天宫课堂”第二课。据此完成下面小题。
1.3月23日“天宫课堂”开讲时,在伦敦留学的小明手表时间是()
【解析】1.据材料可知,北京时间3月23日15:40神舟十三号的3名航天员在中国空间站讲授了“天宫课堂”第二课,北京时间即东八区区时,据所学知识可知,伦敦位于零时区,两地相差8个时区,所以按照“东加西减”的方式,3月23日“天宫课堂”开讲时,在伦敦留学的小明手表时间为23日7时40分,A正确;BCD错误。故选A。
(2023·河南·模拟预测)北京时间2022年4月16日09时56分,神舟十三号载人飞船返回舱在内蒙古东风着陆场成功着陆,着陆点中心地理坐标为(41°37'43”N,100°04'28”E)。现场医监医保人员确认航天员翟志刚、王亚平、叶光富身体状况良好,神舟十三号载人飞行任务取得圆满成功。据此完成下面小题。
2.神舟十三号载人飞船返回当日,与内蒙古相比,云南()
4.三位航天员重返地面时,与北京处于同一日期的范围占全球范围的比例()
【解析】2.地球自转角速度,在地球上除极点外,各地都相同,A错误;云南所处纬度比内蒙古低,4月太阳直射点位于北半球,云南距离太阳直射点更近,正午太阳高度更大,B正确;自转线速度由赤道向两极递减,因此云南比内蒙古线速度大,C错误;太阳直射点位于北半球,北半球纬度越高昼越长,内蒙古昼更长,D错误。故选B。
3.国际标准时为0时区,北京时间2022年4月16日09时56分,即东八区为4月16日09时56分,0时区位于东八区西侧且相差八个小时,根据“东加西减”,国际标准时间为2022年4月16日1:56,A正确。故选A。
4.北京时间2022年4月16日09时56分,即东经120度的地方时,此时对应180度经线的地方时为4月16日09时56分+4小时=4月16日13时56分,则4月16日占全球的比例为13时56分/24小时,约为7/12。B正确。故选B。
(2021·天津·高考真题)科考队在北极圈内某地进行科考时,于北京时间6月22日16时测得了当地一天中太阳高度的最小值为10°。完成下面小题。
【分析】5.6月22日是夏至日,太阳直射点位于北回归线,该地为北极圈以内,有极昼,一天中最小太阳高度为10°,为0:00的太阳高度,此时北极圈上0:00的太阳高度0°,从而得出该地的纬度为北极圈以北10°,即76°34′N,故C项正确,ABD错误。故选C。
6.由材料可知,此时为6月22日(夏至日),北极圈及其以北地区出现极昼现象,因此该地出现一天中最小太阳高度时,地方时应为24时,而此时北京时间为16时,说明与北京所在时区相差八个时区,每时区经度相距15°,由此可得出该地经度约为120°W,选项中符合条件的只有北美北部。故A,B,C项错误,D项正确。故选D。
【点睛】极圈内刚好发生极昼的纬度与直射点纬度互余,该纬度0:00的太阳高度为0°,如果给出极圈内某地0:00的太阳高度,求该地的纬度,就将刚好发生极昼的纬度加上该地0:00的太阳高度,就可以得出该地的纬度。
(2023·江苏·模拟预测)小海坨山位于延庆县西北部,呈东南——西北走向,是2022年北京冬奥会的重要赛区之一。读下图,完成下面小题。
7.图示区域最高点为小海坨主峰,海拔为2241米,最低点位于图示区域东南,海拔为0~500米。因此图示区域最大海拔差可能是接近2241米,D正确,ABC错误。故选D。
(2023·全国·模拟预测)下图是“我国某地附近等高线图及某绳降照片”。读图,完成下面小题。
8.某极限运动俱乐部在A处从崖顶到崖底开展绳降比赛,运动员准备的绳长最适宜的是()
【分析】8.图中等高距为20米,A处有四条等高线重叠,则该处陡崖相对高度介于60至100米之间,为安全考虑,绳长应略大于100米较合适,B正确,ACD错误。故选B。
(2021·北京·高考真题)我国某镇利用当地主产的粮食制作粮画,打造粮画小镇。图a是M学校设计的小镇地理位置指示牌,图b是该校设计的四条“行走的思政课”精华路线示意图。读图,完成下面小题。
【解析】9.图中最短精华路线是从M学校至传统民居保护地这条线路,根据图中比例尺进行计算,图上1厘米代表实际距离5千米,可以计算出最短的精华路线里程约为10千米,B项正确。故选B。
【点睛】比例尺计算公式:实际距离=图上距离&pide;比例尺
(2023·全国·模拟预测)公元前814年,以航海经商著称的腓尼基人兴建迦太基城。公元前264年为争夺海上交通枢纽西西里岛,与罗马帝国交战失败,史称“第一次布匿战争”。公元4~16世纪期间迦太基沦为拜占庭等国家属地,迦太基商贸地位逐渐衰落。下图为迦太基势力范围示意图。据此完成下面小题。
10.从罗马经西西里岛西端至迦太基的最短距离约()
【解析】10.根据题意观察图中信息,罗马到迦太基的距离大约跨越纬度5°(按照跨越35°-45°大约估算),而地球的经线圈都是相同的周长,主要以本初子午线所在经线圈计算,大致为40007千米,一周为360°,则跨越1°纬度实际长度大约为111千米,则罗马到迦太基的最短距离大约为111.1×5≈555千米,ABCD四个选项中,只有B选项500千米最接近答案,故B正确。答案选择B。
(2023·北京·模拟预测)下图为某年7月赴北极科考的“雪龙二号”科考船的一日航行轨迹图。读图,完成下列小题。
【解析】11.根据图中信息,该日“雪龙二号”的航行路径大致跨越了两个纬度,四个经度,大致可以得出其两个直角边的距离为222km左右,线路为其斜边,约为300km左右,C正确,ABD选项均差距过大。故选C。
(2021·江苏·高考真题)公元8世纪开始,基尔瓦逐渐成为非洲东海岸的商贸中心。15世纪初郑和船队曾从不同航线到达基尔瓦。17、18世纪随着世界贸易格局不断改变,基尔瓦商贸地位逐渐衰落。1981年基尔瓦所在地的遗址被列入世界遗产名录。图为“郑和船队航海路线示意图”。据此完成下面小题。
12.郑和船队若每天航行190km,从科伦坡经摩加迪沙至基尔瓦的最短时间约()
【解析】12.据图中经纬线可知,从科伦坡到摩加迪沙大致经过35个经度距,且位于赤道附近,故两地距离可计算为111×35=3885km,从摩加迪沙到基尔瓦大致经过10个纬度距,可计算两地距离为10×111=1110km,故从科伦坡到基尔瓦距离大致为4995km,据材料,郑和船队每天航行190km,可计算大致需要27天能到达,故最短4周就可到达,B项正确,ACD错误。故选B。
(2022·江苏·高考真题)国际空间站距地面约420km,每90分钟环绕地球一周。空间站反射阳光,在一定条件下,人们肉眼可以看到明亮的光点划过天空。下图为“国际空间站某时段轨迹和某时刻位置示意图”,图中阴影表示黑夜。据此完成下面小题。
【解析】13.由图可知北京与国际空间站经度大致相差180°,所以国际空间站到达北京上空是大致绕地球旋转了一半,由材料可知国际空间站每90分钟环绕地球一周,所以空间站到达北京上空约需45分钟。故C正确ABD错误。故答案选C。
14.由下图可知图中A点与120°E相距约为60°,A点为晨线与赤道的交点,则A点地方时为6时,则北京时间此时约为10:00,结合上面分析,可知空间站到达北京上空时,北京时间大致为10:45,故C正确ABD错误。故答案选C。

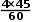 =15:00,以B点作为已知时间点求F点的地方时为24:00—
=15:00,以B点作为已知时间点求F点的地方时为24:00—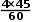 =21:00
=21:00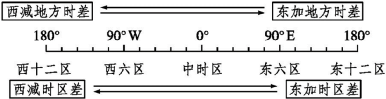
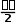 ;日落时间=12+
;日落时间=12+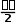







-lp.jpg)
-lp.gif)
-lp.jpg)
